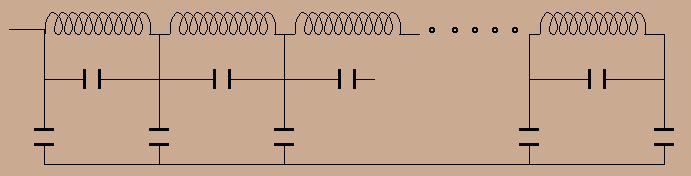
We have seen how leakage inductances of windings can be computed (or at least estimated). It's clear that those inductances will tent to limit performances of a transformer in high frequencies. To make that point more precise, we will enrich the original equivalent schema of the real transformer. First of all, it must be noticed that winding a wire on a core creates both inter-turns and inter-windings capacitances. A winding can thus be seen as a trasnmission line :

Complete computation of propagation modes along such a line is possible, but tedious unless inter-turns capacitance is neglected. Generally however, a winding is heavily damped and we can assume without problem that spread capacitances can be modelled as localized components. This yields to the following schema (we neglect leakage resistance between windings and core!) :
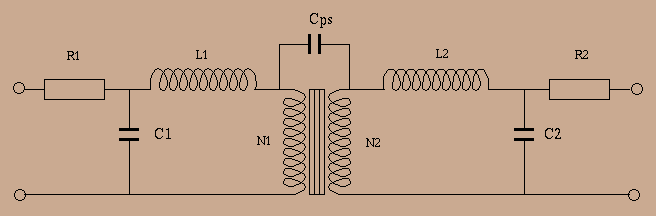
At low frequencies, one can neglect the effect of parasitic
capacitances, and , assuming a pure resistive load ![]() at the
secundary, the system of equations (5) gives an approximate schema :
at the
secundary, the system of equations (5) gives an approximate schema :
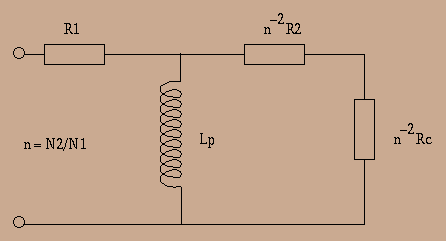
Where ![]() is primary inductance, that is self-inductance of the
primary winding alone (linked to
is primary inductance, that is self-inductance of the
primary winding alone (linked to ![]() in (5), that cannot be
neglected at low frequencies), which can be computed knowing core
parameters (see section on reluctance). We have then a high-pass
filter, and putting :
in (5), that cannot be
neglected at low frequencies), which can be computed knowing core
parameters (see section on reluctance). We have then a high-pass
filter, and putting :
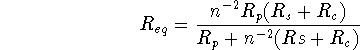
the low cut frequency is :
![]()
Note
If input generator's impedance is non zero, one must add it to
![]() . In the case of a valve amplifier output transformer, that
impedance will be the plate resistance of the output tube.
. In the case of a valve amplifier output transformer, that
impedance will be the plate resistance of the output tube.
For high cur, we will not include in our computation the parasitic capacitances of windings. We have then the schema :
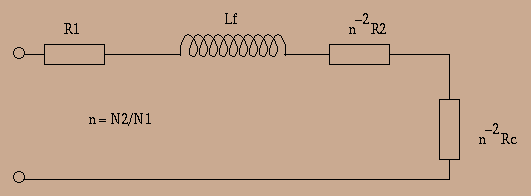
Where ![]() is total leakage inductance seen at primary.
We have now a low-pass filter whose cutting frequency is, putting :
is total leakage inductance seen at primary.
We have now a low-pass filter whose cutting frequency is, putting :
![]() , given by :
, given by :
![]()
If parasitic capcaitances are taken into account (and reduced to
primary by ![]() ), it will appear a damped LC
circuit of oscillating frequency :
), it will appear a damped LC
circuit of oscillating frequency :
![]()
Generally, this frequency is higher than high-cut created by leakage
inductances and its effect consist mainly in slightly lowering
band-pass. In some rare occasions, damped oscillations can appear (to
be controlled on square wave with a scope).