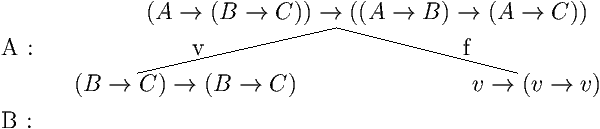4 Démonstration
A|= B : B est vrai si A
A|- B : B est prouvable à partir de A
Logique = ``A|= B ssi A|- B''
| Syntaxe |
Sémantique |
| Formule |
Fonction |
| Démonstration |
Modèle |
| Axiomes, règles d'inférence |
Table de vérité |
| Théorème |
Tautologie |
| Déduction |
Conséquence valide |
| |- |
|= |
4.1 Méthode axiomatique
Définition 12
Une démonstration est une suite de formules A1...An telle que :
-
soit Ai est l'instance d'un axiome ;
- soit Ai est le résultat de l'application d'une règle d'inférence sur
Ai1...Aik avec ii<i...ik<i.
| Axiomes |
Règles |
| A ® (B ® A) |
modus ponens |
| (A ® (B ® C)) ® ((A ® B) ® (A ® C)) |
|- A |- A ® B/|- B |
| (¬ B ® ¬ A) ® (A ® B) |
|
Exemple : preuve de p ® p.
Définition 13
Déduction : A1... An |- B : en ajoutant les axiomes A1...An, B est un théorème (``on peut prouver B avec les hypothèses
A1... An'').
Propriété 9
Théorème de déduction : A|- B ssi |- A ® B.
Preuve : Ü : une application de MP. Þ : théorème
de Herbrand, preuve par induction sur la hauteur h de l'arbre de
preuve :
-
Si h=0. nécessairement A=B, or |-A ® A
- h>0, l'arbre de A |- B a la forme suivante :
Par induction, on a |- A ® X et |-A ® (X ® B)
D'où
|
|
| |-A ® X
|
| |-A ® (X ® B)
|-a ® (b ® c) ® ((a ® b) ® (a ® c)) |
|
| |-(A ® X) ® (A ® B) |
|
|
|
| |- A ® B |
|
4.2 Propriétés
Définition 14
Une théorie de la preuve (|-) est dire correcte si tout théorème
A (|- A) est une formule valide (|= A).
Propriété 10
La méthode axiomatique est correcte pour le calcul propositionnel.
Preuve :
-
les axiomes sont des tautologies ;
- la règle du Modus Ponens est correcte (exercice).
Définition 15
Une théorie de la preuve est dite consistante s'il n'existe pas de
formule A telle que |- A et |- ¬ A.
Propriété 11
La méthode axiomatique est consistante.
Définition 16
On dit qu'un théorie de la preuve (|-) est complète ssi pour
toute formule A, si |= A alors |- A.
Propriété 12
La méthode axiomatique est complète. On dit aussi que le calcul propositionnel
est complet.
Preuve : Avec une autre méthode de démonstration...
Définition 17
Informelle : une théorie est décidable s'il existe un algorithme qui étant
donnée une formule A décide si |- A ou si non |- A.
Propriété 13
Le calcul des propositions est décidable.
Preuve : Exercice
4.3 Calcul des séquents
Idée : pour montrer qu'une formule est une tautologie, on montre qu'aucune
valuation ne satisfait sa négation. Pour cela on manipule deux ensembles
de formules : celles qui doivent être fausses (à droite) et celles qui
doivent être vraies (à gauche).
Exemple : (A ® B) ® (¬ B ® ¬ A)
4.3.1 Définitions
Définition 18
Un séquent est une paire d'ensembles finis de
formules : G ¾® D, G est l'antécédent, D le conséquent.
Intuitivement, A1... An ¾® B1... Bm s'interprète comme la formule
A1 Ù ... An ® B1 Ú ... Bm, i.e. un séquent est faux si tous les
Bi sont faux et tous les Ai sont vrais.
Définition 19
Une règle d'inférence est constituée d'un ensemble de séquents prémisses
et d'un séquent conclusion
On va construire un arbre dont les noeuds sont étiquetés
par ces règles.
Système G de Gentzen
(A et B sont des formules, G
et D sont des ensembles de formules) :
|
|
|
Ù G
|
| G ¾® A,D G ¾® B,D |
|
| G ¾® A Ù B, D |
|
Ù D
|
|
|
| A, G ¾® D B, G ¾® D |
|
| A Ú B, G ¾® D |
|
Ú G
|
|
Ú D
|
|
|
| G ¾® A, D B, G ¾® D |
|
| A ® B, G ¾® D |
|
® G
|
| A, G ¾® B, D |
|
| G ¾® A ® B, D |
|
® D
|
Définition 20
On dit que le séquent A1... An ¾® B1... Bm est falsifiable
ssi il existe une valuation I telle que
I|= A1 Ù ... Ù An Ù ¬ B1 Ù ...¬ Bm
On dit que le séquent A1... An ¾® B1... Bm est valide ssi
|= A1 Ù ... An ® B1 Ú ... Bm
Propriété 14
Les règles du système G sont correctes : le séquent conclusion est valide
ssi les séquents prémisses sont valides.
Preuve : Exercice
4.3.2 Arbre de preuve
Définition 21
Un axiome est un séquent G ¾® D tel que GÇD¹Ø.
Remarque : un axiome est un séquent valide.
Définition 22
Arbre de déduction : tous les noeuds sont des règles.
Arbre de preuve : arbre de déduction dont les feuilles sont des axiomes.
Exemple : ¾® ((A ® B) Ù A) ® B
Exercice : Donner la règle d'inférence pour le connecteur ou-exclusif
Å=l pq.((p Ù ¬ q) Ú (¬ p Ù q))
Définition 23
On dit qu'un séquent est prouvable si on peut construire un arbre de preuve
dont il est la racine.
Propriété 15
Le système G est correct (sain), i.e. un séquent prouvable est valide.
Preuve : par induction sur l'arbre de preuve.
En pratique :
-
Pour montrer |= A, on prouve |= ¾® A ;
- Pour montrer A |= B, on prouve |= ¾® A ® B.
4.3.3 Recherche de preuve et complétude
Algorithme de recherche d'un arbre de preuve T pour un séquent
G ¾® D :
-
Initialisation : T:=G ¾® D
- Choisir dans T une feuille qui contient au
moins une formule non atomique, lui appliquer une règle, recommencer.
- Si le choix est impossible :
-
si toutes les feuilles sont des axiomes, le séquent initial est valide
- sinon, le séquent initial est falsifiable
Exemple : ¾® (p Ú (q ® p)) ® (p Ú ¬ q),
¾® (p ® q) ® (q ® p).
Propriété 16
La procédure de recherche termine. Si le séquent initial est valide alors
l'arbre obtenu est un arbre de preuve. S'il est falsifiable, on obtient un
contre-exemple en falsifiant la feuille qui n'est pas un axiome.
Corollaire : le système G est complet
4.4 Méthodes sémantiques
Ce n'est pas à proprement parler de la démonstration mais plutôt de l'évaluation.
4.4.1 Arbre
Méthode identique aux tables de vérités mais sous forme d'arbre : chaque
niveau de l'arbre correspond à une variable.
Exemple : ((p ® q) Ù q) ® q
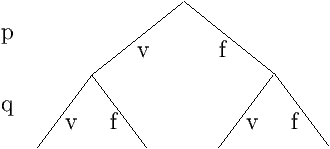
Algorithme de Quine : on évalue partiellement la formule au fur
et à mesure de la création de l'arbre.
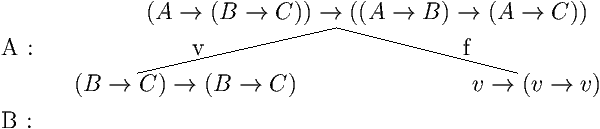
4.4.2 Forme clausale
Rappel : Toute formule admet une forme normale conjonctive.
Définition 24
On appelle clause une disjonction de littéraux. On notera une
formule sous forme normale conjonctive comme un ensemble de clauses.
4.4.3 Algorithme de Davis & Putnam
Méthode analogue à Quine sur la forme normale conjonctive.
Calculer la forme normale conjonctive N de la formule à prouver.
-
Si N est vide, succès.
- Si une clause de N est vide, la formule n'est pas satisfiable
- Choisir une variable p, calculer Np (resp. N¬ p)
l'ensemble des clauses de N où p (resp. ¬ p) apparaît, Nc le reste.
- Calculer Np (resp. N¬ p) en supprimant
p dans Np (¬ p dans N¬ p).
- Répéter récursivement avec NpÈ Nc et N¬ pÈ Nc
Preuve : N est satisfiable ssi NpÈ Nc ou N¬ pÈ Nc le
sont.
Heuristiques :
-
Si une clause ne contient qu'un seul littéral, le choisir.
- Choisir la variable qui a le plus d'occurrences.
4.5 Résolution
Rappel : A1,...,An|= A ssi A1 Ù ... Ù An Ù ¬ A
est insatisfiable.
Donc toute preuve de déduction peur se faire par preuve d'insatisfiabilité :
principe de réfutation.
Propriété 17
Soient C1 et C2 deux clauses et p un atome tel que pÎ C1 et
¬ pÎ C2. On appelle R=C1\pÈ C2\¬ p la
résolvante de C1 et C2.
{R,C1,C2} º {C1,C2}
C'est le principe de résolution.
Preuve : (A Ú p) Ù (B Ú ¬ p)|= A Ú B
(exercice)
Propriété 18
La résolution est complète pour la réfutation : en partant d'un ensemble de
clauses insatisfiable, on obtient la clause vide par application répétée du
principe de résolution.
Exemple : {p ® r,q ® r}|=(p Ú q) ® r
4.5.1 Clauses de Horn
Définition 25
Une clause de Horn est une clause comportant un littéral positif au plus.
Exemple : p, p Ú ¬ q Ú ¬ r, ¬ p Ú ¬ q, p Ú q.
Algorithme de résolution pour les clauses de Horn. Soit N l'ensemble
de clauses dont on veut prouver la non satisfiabilité.
-
Si ØÎ N, N est insatisfiable (succès pour une
réfutation)
- Sinon, choisir {p}Î N et CÎ N tel que ¬ pÎ C, calculer
C\{¬ p} la résolvante de {p} et C, continuer avec
N\ CÈ
{R}
- Sinon N est satisfiable (échec pour une réfutation)
Remarque : on peut supprimer C de N car C est une conséquence
logique de R.
Exemple : {¬ p Ú r, ¬ r Ú s, p, ¬ s}